Acoustic Properties of Rectangular Rooms

Contents

Introduction 
Room Modes 
          The Issues Created by Room Modes and Common Solutions 
          The Schroeder Frequency 
          Axial, Tangential and Oblique Modes 
          Tackling Room Modes for the End User 
Room Size and Ratio 
          The Issues Created by Room Ratios and Common Solutions
          Old and New Methods for Determining Optimum Ratios
          Large vs. Small Rectangular Rooms 
Building Materials 
          How A Sound Wave Will Interact with a Material
          Room Resonances with Regards to Building Materials
          Reflectors, Absorbers and Diffusers 
          Absorption Coefficient 
          Porous vs. Nonporous Absorbers 
Conclusion 
References 

Introduction

In the modern day, significant importance has been placed on the acoustic quality of critical listening spaces. Offsetting acoustic abnormalities is useful for professional critical listening spaces so that they may fulfil their purpose of allowing a person to listen to a source appropriately. These abnormalities affect a room’s acoustic quality in the context of modes and can include, but are not limited to size, ratios, and building materials. Discussing and suggesting ways to reduce the effects of these variables is the purpose of this report. Relevant information on these sub-topics is explored to inform and educate the reader on this subject so that they may treat their space accordingly.

Room Modes

The Issues Created by Room Modes and Common Solutions
Room modes refer to an irregular perceived frequency response of a room due to specific frequencies reflecting on themselves between parallel walls, this can also be called “colouration.” Colouration can be particularly apparent with lower frequencies as room modes are less densely packed at this range. This effect can be alleviated by altering the position of the source and listener in the room, but this on its own will not completely negate the issue. [1] M. Louden outlines this phenomenon, where he notes that a particularly bad case of an irregular frequency response is when eigentones group at lower ranges which can leave large gaps in other areas of the frequency spectrum. This results in a room which has an ununiform acoustic response. [2] This becomes an issue because, for the listener, the acoustic quality of the room is altered, as the frequency content of small critical listening spaces can be over or underrepresented in specific ranges. [3] In the context of a recording studio, this creates weak frequencies which, if they represent specific musical notes, can be under-represented and therefore can be mistreated in a mix by the engineer. [4] (1) Variable frequency responses can be addressed by controlling sound reflections with passive acoustic treatment such as bass traps, membrane absorbers and Helmholtz resonators. [3]
The Schroeder Frequency
The Schroeder frequency refers to the transitional region of the frequency response of a room that distinguishes the lower frequencies which consist of separate modes from the higher frequencies which consist of densely overlapping modes. [5] This phenomenon was investigated by Manfred Schroeder and in 1962 he came to an equation that estimated this region of overlap. [6] Estimating this frequency is useful in situations where an acceptable degree of homogeneity in the sound field is required for study or design, such as the design of a reverberation room. It is important for the Schroeder frequency to be considered in rooms with smaller volumes in particular, as larger spaces do not share the same diffusion properties as smaller spaces. [7]
Axial, Tangential and Oblique Modes
Axial, tangential, and oblique modes can be described as modes that exist in different planes. Being mindful of these different modes can help recognise the redistribution of energy these modes can create. [8] These distinct types of modes are also known as natural frequencies, standing waves and normal modes, respectively. [4] (1)

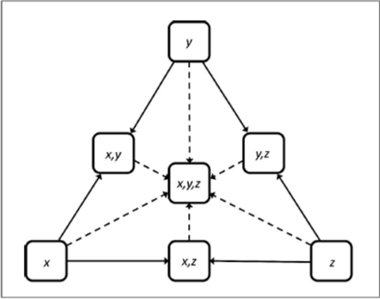
Diagram cited from [8] 3.1 Coupling between modes due to scattering, Figure 8
-Axial modes are modes that exist in one dimension, two surfaces of the room, these are boxes “x”, “y” and “z” in the diagram above.
-Tangential modes are modes that exist in two dimensions, four surfaces of the room, these are boxes “x,y” “y,z” and “x,z” in the diagram above.
-Oblique modes are modes that exist in three dimensions, six surfaces of the room, this is represented as box “x,y,z” in the diagram above.
Tangential modes such as “x,y” cannot interact with “z” and vice versa as they do not share reflecting surfaces.
The diagram should help to illustrate that axial, tangential and oblique modes can interact with each other and therefore transfer energy, which is called “coupling.” Coupling results in a difference in perception of frequency response and therefore should be considered when addressing this problem. [8] It should also be noted that more complex modes such as oblique modes create complications when predicting aspects of acoustics, such as the prediction of modal reverberation times. [9]
Tackling Room Modes for the End User
The tackling of room modes for the end user can vary depending on the purpose of the space. Whilst a completely even distribution of modes in a recording studio may be desired, this may not be sought after in a room such as a home cinema. In this situation, a sterile listening environment would not aid a listener’s entertainment experience so it may be beneficial for modes localised in lower frequencies to be left to create a “fuller” listening experience. [10] In many cases, it is difficult to implement measures to help the acoustics of a space simply due to the limitations of the design of our spaces. Practically, floors need a good amount of area, surfaces need to be robust and building costs need to be as low as possible. Gravity causes logistical issues with building slanted surfaces and most people would not enjoy standing on a floor that is not completely horizontal. It is for this reason that, in general, the tackling of room modes for critical listening spaces that are not purpose-built is limited to adding acoustic treatment onto surfaces. [11] Nevertheless, acoustic treatment can be useful in both the recording studio and in public spaces where the intelligibility of the source is the key issue. Treatment can be useful in improving the intelligibility of a mix in a control room as well as the intelligibility of speech in a traffic terminal. [12]

Room Size and Ratio

The Issues Created by Room Ratios and Common Solutions
The fundamental principle of room ratios of small rooms is that room ratios that are simple and even, such as a perfect cube 1:1:1 will have an irregular frequency response at low frequencies due to an uneven distribution of eigentones. It is for this reason that many researchers have tried to determine a ratio that has an optimal eigentone distribution. [2] Finding these uneven distributions involves conducting impulse response tests which take into consideration the positions of the source and receiver within the room. A best-fit curve of the frequency response of a room that has less prominent variations has better acoustic quality and this is a quantifiable way in which rooms with varying room ratios can be compared. [13] Sterile listening spaces such as recording studios can benefit greatly from optimum room dimensions and geometry to tackle the colouration of the audio being listened to. [14] A common solution to problems in recording studios created by room ratios is to create unparalleled walls that change direction at even intervals. This is not a complete solution as no shape can create a perfect room, however, this approach does work in many instances of its application. Additionally, selecting a room ratio that has both symmetry and is known to have a good low-frequency response due to its modal distribution will be favourable to an engineer. [10]
Old and New Methods for Determining Optimum Ratios
It should be noted that many methodologies have been proposed before, in between and after the methodologies presented in this section. This section serves as a brief history of old and new methods for determining optimum room ratios.
The optimisation of room ratios began as far back as ancient Greece with the Golden Ratio, a mathematical term describing a consistent proportion which is found in nature, architecture, art, and music. This Ratio is 1:1.6:2.6 and was thought at the time as a solution to optimum room acoustics. [15] In the 1946 R.H. Bolt suggested that a ratio of 2:3:5 would result in a more even spacing of room modes which was determined by producing design charts. [16] In 1981, O. Bonello suggested a new method that a ratio that possessed an increasing number of modes in one-third octave bands as the frequency increased would be optimal. This criterion was introduced so that colouration was at least minimised, as eigentones being concentrated and absent in varying parts of the spectrum was the root of the problem. [17] In 2001, T. J. Cox and P. D’Antonio proposed a new method which acts directly on the modal response of the room, which means that the criterion based on modal spacing used by previous methods was not required. This new method also set itself apart as it was able to consider the different effects of absorption of axial, tangential and oblique modes which previous methods could not. Their new method was derived from computer algorithms generating optimum ratios which were considerably flatter when compared against the golden ratio, Bolt’s 2:3:5 ratio and ratios determined by Bonello. [18] Finally, in 2017 M. Meissner suggested a new method which was representative of the source and receiver positions as well as the evenness of the frequency response among different receiving positions. This method calculated a best-fit curve using the quadratic polynomial regression and then compared the deviation of computed curves to the best-fit curve to determine a ratio with an optimal frequency response. This method concluded that ratios 1:1.48:2.12, 1:1.4:1.89 and 1:1.2:1.45 were optimal in rooms that had a volume less than or equal to 150 cubic meters. [13]
Large vs. Small Rectangular Rooms
The acoustic properties of a large room are significantly different to that of a small room. This is, in part, due to the location of their Schroeder frequencies as touched on previously. The Schroeder frequency of a large room such as a church may lie around 30Hz, whereas a classroom may lie around 140Hz. A church therefore has an overlapping of room modes which spans across the entirety of the relevant frequency range which makes it difficult to assess eigenfrequencies. The classroom’s acoustic properties in the low end are affected by the frequencies below its Schroder frequency which makes it considerably more complicated in relation to predicting its acoustic performance. [19] Other problems regarding size and proportions are linked to resonant frequencies and coupling. The size of a rectangular room is linked to the spacing of resonant frequencies where the smaller the room becomes, the further apart these frequencies are spaced which can create resonance. There is also the problem created by coupling which occurs when rooms that are connected to other untreated rooms influence the acoustic quality of the main room. This can be particularly troublesome in larger spaces such as churches or theatres as these are usually connected to, but not separated from stairwells, entrances, and smaller spaces without doors. This is also a problem for smaller rooms such as recording studios where a treated critical listening space connected (without obstruction) to an untreated space such as a hallway to a live room will have an adverse effect on the acoustic quality of the treated space. [4] (2)

Building Materials

How A Sound Wave Will Interact with a Material
All rooms, regardless of the materials used in the walls will result in a loss in energy for a sound source every time it reflects off a surface of the room. This means that all sound waves, including standing waves, will eventually dissipate into silence. [19] There are several varying ways in which a sound source will interact with a room’s building materials during the time it takes to be dissipated completely which will be explored in this section.
Room Resonances with Regards to Building Materials
The resonance of a room is linked to the materials the room is comprised of. Detectable resonant frequencies are the result of the average spacing of eigenfrequencies being larger than the half-width of the resonances. A small, tiled bathroom has this exact characteristic where the resonant frequencies are individually excitable if evoked. Conversely, a wooden room does not share a similar spacing of eigenfrequencies, and so has resonances which are difficult to pick out. Their overlapping, or lack of overlapping resonant frequencies is the reason the two rooms can be distinctly different in their acoustic qualities. [19] Room resonances can be problematic in day-to-day situations such as teachers in classrooms being difficult to interpret due to loud background noise exciting resonances which have long reverberation decay times. The most practical solution to this is the implementation of acoustic treatment. [20]
Reflectors, Absorbers and Diffusers
There are several ways in which sound may interact with treated room walls. Reflection is when a sound wave reflects off the wall either back on its path, or in a different direction. Absorption is when a sound wave is reduced in energy by a wall which as a result reduces the loudness of the reflected wave. Diffusion is when a sound wave is scattered by the wall which leads to a uniformity in the reflection of that sound wave. The diagram below should help to illustrate the different results of these reflected, absorbed, and diffused waves. Materials that can absorb and diffuse sound waves effectively are known as absorbers and diffusers respectively, and a combination of both will help to treat critical listening spaces. Specifically, a combination of both will reduce the prevalence of colouration, echoes, stereo image shifting, and frequency intelligibility. [21]
Below is a diagram to illustrate the difference between these materials.

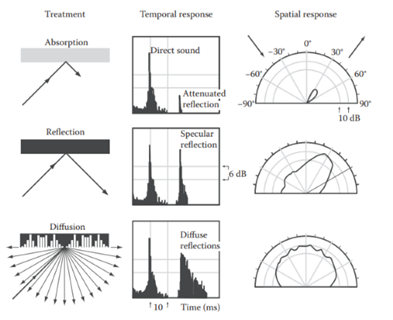
Diagram cited from [21] Acoustic Absorbers and Diffusers Chapter 1, p.2, Figure 1.1
A phenomenon which may aid the acoustic quality of larger spaces is called intimacy. Intimacy refers to early reflections of a sound source arriving at the listener directly after the initial source arrives which creates an enhancement of speech or music. Reflections that arrive side-on to the listener as opposed to overhead are particularly desirable as this creates a stereo effect for the listener. Recreating intimacy in a space such as a theatre includes built-in or suspended reflectors on the walls or ceilings and building materials that do not create unnecessary resonance, absorption, or high-frequency reflections. [22] (1)
Absorption Coefficient
With regard to room modes, the specific building materials used can have an impact on the time that it takes for a standing wave to dissipate. This can be described as the material’s absorption coefficient. [13] The absorption coefficient is a measure of the efficiency of sound absorption of a surface or material. If 55 per cent of the incident sound energy is absorbed, the absorption coefficient is said to be 0.55. Air has the highest possible coefficient of 1. [4] (3) It is possible for several different absorption coefficients to be ascertained from a room’s surfaces, but in practice, this is not taken into account when describing a room’s absorbing properties. [23] Therefore, the absorbing properties of a room can be described as the mean absorption coefficient of its surfaces. [13] The absorption coefficient of a material is a useful term, not only because it is a unitless quantity between zero and unity, but it is also likely to be the most widely used quantity when describing absorbent materials. Most absorbent materials are often presented in a graph of absorption versus frequency to illustrate their absorption properties. [24]
Porous vs. Nonporous Absorbers
A wide range of sound-absorbing materials exist which provide absorption properties depending on frequency, composition, thickness, surface finish and the method they are mounted. However, materials that have a high sound absorption coefficient are usually porous. [25] With regards to acoustic absorption the most relevant difference between porous and nonporous materials is their specific frequency absorption. Porous absorbers such as acoustic foam, oak, or carpets are more effective at absorbing frequencies above 500Hz which is governed by a logarithmic curve. Low-frequency absorption can be improved by increasing the distance of the absorber from the wall and the effectiveness of porous materials will be reduced if they are painted. In contrast, nonporous materials such as treated woods, glass, ceramics, or metal can be effective at absorbing lower frequencies. Creating space between the wall and the absorber and introducing a porous absorber in the space in between can increase the effectiveness of low-frequency absorption dramatically. A careful and informed choice between the allocation of these materials is essential to creating a tailored space that fits its desired purpose. [22] (2)

Conclusion

With sufficient knowledge, it is within a person's capability to acoustically treat a space adequately. A person’s most notable issue to tackle is room modes which will greatly change their perception of the acoustics of their space. However, with the right countermeasures including bass traps, membrane absorbers and Helmholtz resonators and an understanding of the Schroeder frequency and the coupling of modes that exist within different planes, tackling room modes should not be a daunting task. Also, ideas relating to the issues created by room ratios, resonances, and room volumes, would be invaluable to treating a space correctly. Finally, being familiar with optimum ratios, reflectors, absorbers, diffusers, porous and nonporous absorbers, and the absorption coefficient of a room would all open steps towards treating a space effectively.

References

[1] Acoustics. (n.d.). Room sizing for studios | Acoustics | University of Salford. [online] Available at: https://hub.salford.ac.uk/sirc-acoustics/architecture-and-building-acoustics/room-sizing-for-studios/.

[2] Louden, M.M. (1971). Dimension-Ratios of Rectangular Rooms with Good Distribution of Eigentones. Acta Acustica united with Acustica, [online] 24(2), pp.101–104. Available at: https://www.ingentaconnect.com/contentone/dav/aaua/1971/00000024/00000002/art00007.

[3] Bistafa, S., Hodgkin, M., Morita, W., Köhn, B. and Neto, J. (2012). Adaptive Control of Low-Frequency Acoustic Modes in Small Rooms. The Open Acoustics Journal, [online] 5, pp.16–22. Available at: https://benthamopen.com/DOWNLOAD-PDF/TOACOJ-5-16/[Accessed 3 Apr. 2024].

[4] Frederick Alton Everest (1989). The Master Handbook of Acoustics. Tab Books.
1. pp. 84-101. Chapter 6. Sound Indoors – a’ la mode
2. pp. 254-255. Chapter 14. Acoustics of the Home Listening Room
3. p. 159. Chapter 10. Absorption Of Sound – Absorption Coefficient[5] Skålevik, M. (2011). Schroeder Frequency Revisited Schroeder Frequency Revisited. [online] Available at: https://www.akutek.info/Papers/MS_Schroeder_Revisited.pdf.

[6] Schroeder, M.R. and Kuttruff, K.H. (1962). On Frequency Response Curves in Rooms. Comparison of Experimental, Theoretical, and Monte Carlo Results for the Average Frequency Spacing between Maxima. The Journal of the Acoustical Society of America, 34(1), pp.76–80. doi: https://doi.org/10.1121/1.1909022.
[7] De, M., Gomes, A., Bonifacio, P., Brandao, E., Sant'ana, L., Bertoti, E., Catai, R., Hilbeth, A. and De Deus (n.d.). Crossover frequency estimation from statistical features of a room transfer function. [online] Available at: https://pub.dega-akustik.de/ICA2019/data/articles/001103.pdf[Accessed 3 Apr. 2024].

[8] Rindel, J.H. (2015). Modal Energy Analysis of Nearly Rectangular Rooms at Low Frequencies. Acta Acustica united with Acustica, 101(6), pp.1211–1221. doi: https://doi.org/10.3813/aaa.918914.
[9] Rindel, J.H. (2016). A Note on Modal Reverberation Times in Rectangular Rooms. Acta Acustica united with Acustica, 102(3), pp.600–603. doi: https://doi.org/10.3813/aaa.918977.
[10] Ballou, G. (2013). Handbook for Sound Engineers, 4th Edition. Focal Press, pp.138-142.
[11] Skålevik, M. (n.d.). Small Room Acoustics -The Hard Case. [online] Available at: https://www.akutek.info/Papers/MS_Hard_Case.pdf [Accessed 3 Apr. 2024].
[12] Ismail, L. (n.d.). Acoustic and durability performances of Arenga Pinnata panel. core.ac.uk. [online], pp. 7-10. Available at: https://core.ac.uk/display/12007262 [Accessed 3 Apr. 2024].
[13] MEISSNER, M. (2018). A Novel Method for Determining Optimum Dimension Ratios for Small Rectangular Rooms. Archives of Acoustics, [online] 43(2). Available at: https://acoustics.ippt.pan.pl/index.php/aa/article/view/2198 [Accessed 3 Apr. 2024].
[14] Fett, B. (2006). An In-depth Investigation of the Divine Ratio. The Mathematics Enthusiast, 3(2), pp.157–175. doi: https://doi.org/10.54870/1551-3440.1047.
[15] Cox, T. and D’Antonio, P. (2004). Room Sizing and Optimization at Low Frequencies. [online] University of Salford: School of Acoustics and Electronic Engineering, pp.640–651. Available at: https://www.researchgate.net/publication/28578741_Room_sizing_and_optimization_at_low_frequencies [Accessed 3 Apr. 2024].
[16] Bolt, R.H. (1946). Note on Normal Frequency Statistics for Rectangular Rooms. The Journal of the Acoustical Society of America, 18(1), pp.130–133. doi: https://doi.org/10.1121/1.1916349.
[17] Bonello, O.J. (1981). A New Criterion for the Distribution of Normal Room Modes. Journal of the Audio Engineering Society, [online] 29(9), pp.597–606. Available at: https://www.aes.org/e-lib/download.cfm?ID=3889 [Accessed 3 Apr. 2024].
[18] Cox, T. and D’Antonio, P. (2001). Determining Optimum Room Dimensions for Critical Listening Environments: A New Methodology. [online] University of Salford: School of Acoustics and Electronic Engineering. Available at: https://www.researchgate.net/publication/228530927_Determining_optimum_room_dimensions_for_critical_listening_environments_A_new_methodology [Accessed 3 Apr. 2024].
[19] Kuttruff, H. (2000). Room Acoustics. Fourth Edition ed. Taylor & Francis, pp.73-79.
[20] McKenzie, D.J. and Airey, S. (1999). Classroom Acoustics: E Research Project ; Summary Report. [online] Google Books. Heriot-Watt Univ., Department of Building Engineering and Surveying, pp.1-15. Available at: https://books.google.com/books/about/Classroom_Acoustics.html?id=pfz8tgAACAAJ [Accessed 3 Apr. 2024].
[21] Cox, T.J. and D’antonio, P. (2017). Acoustic absorbers and diffusers : theory, design and application. Boca Raton Crc Press, pp. 1-4.
[22] Kinsler, L.E. and Al, E. (2000). Fundamentals of acoustics. New York: John Wiley & Sons.
1. pp. 347-348. 12.8 Acoustic Factors in Architectural Design. (d) Intimacy.
2. pp.340-341. 12.5 Sound Absorption Materials.
[23] BBC R&D. (1983). A preliminary study of the influence of room mode structure on sound absorption. [online] Available at: https://www.bbc.com/rd/publications/rdreport_1983_04 [Accessed 3 Apr. 2024].
[24] Oldfield, R. (n.d.). IMPROVED MEMBRANE ABSORBERS, pp. 7-8. [online] Available at: https://salford-repository.worktribe.com/OutputFile/1498772 [Accessed 3 Apr. 2024].
[25] Jayamani, E., Hamdan, S. and Suid, N.B. (2013). Experimental Determination of Sound Absorption Coefficients of Four Types of Malaysian Wood. Applied Mechanics and Materials, 315, pp.577–581. doi: https://doi.org/10.4028/www.scientific.net/amm.315.577.

End of report.